Dispersion properties of triply periodic minimal surface stationary phases for LC: The case of superficial adsorption
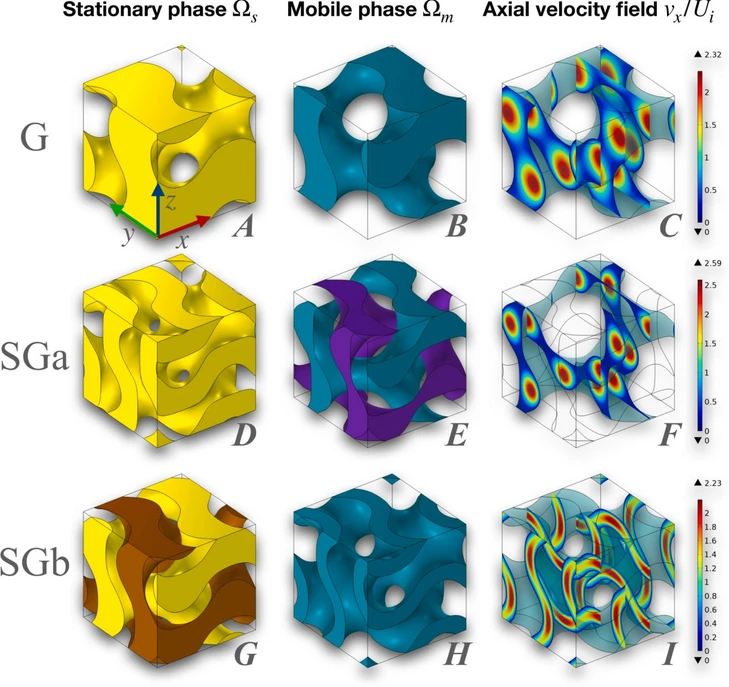
Journal of Chromatography A, Volume 1743, 2025, 465676: Fig. 1. Strut-based Gyroid (G) and sheet-based Gyroids (SGa and SGb): stationary phase (A,D,G), mobile phase (B,E,H) and normalized axial component of the fluid velocity field (C,F,I), being the seepage (interstitial) velocity along x.
The goal of this study is to analyze the dispersion behavior and kinetic performance of eight different 3D-printable stationary phases based on triply periodic minimal surfaces (TPMS), using the exact moment method. Two scenarios were considered: hydrodynamic dispersion in impermeable phases and dispersion under superficial retention conditions. The study calculated dispersion coefficients, plate height curves, and kinetic performance factors.
By examining permeability, tortuosity, and axial velocity uniformity, the researchers identified key geometric traits influencing performance. Among all the structures tested, the sheet-based Gyroid and Primitive geometries showed superior performance, both in terms of kinetic efficiency and reduced void time, making them strong candidates for liquid chromatography applications.
The original article
Dispersion properties of triply periodic minimal surface stationary phases for LC: The case of superficial adsorption
Carolina Lauriola, Claudia Venditti, Gert Desmet, Alessandra Adrover
Journal of Chromatography A, Volume 1743, 2025, 465676
https://doi.org/10.1016/j.chroma.2025.465676
licensed under CC-BY 4.0
Selected sections from the article follow. Formats and hyperlinks were adapted from the original.
The structure of a chromatographic stationary phase plays a crucial role in determining the operational efficiency of the system [1]. For many years, packed beds of spheres have served as a standard in separation technology due to their ease of production and effective performance at a low cost. However, it is now recognized that the theoretical performance of randomly packed beds is inherently restricted by the irregularities within the flow channels and an increasing number of computational studies reveal that ordered stationary phases can reduce band broadening compared to random packing by mitigating eddy dispersion and mass transfer resistance [2], [3], [4], [5], [6], [7]. Ordered geometries for the stationary phase effectively address issues of eddy dispersion and mass transfer resistance by standardizing the internal channel structure of a porous medium. Previous investigations have shown that ordered arrangements of pillars [8], [9], spheres and other regular polygons [4], [10], [11], [12], [13] can theoretically outperform randomly packed beds.
The emergence of additive manufacturing, especially two-photon polymerization printers [14] with minimum feature size order of few hundreds of nanometers [15], represents a significant transformation in our capacity to physically fabricate complex ordered structures that were once nearly impossible to produce. However, ordered packed beds are not optimal for 3D printing, because particles need to be fused and particle–particle contact points, necessary to form a monolithic matrix, are critical points for the structure [13]. 3D printing of porous beds offers the opportunity to design and create ordered monolithic structures optimized to maximize separation performance because it is possible to supersede particle-based structures and produce novel sets of combined solid- and mobile-phase geometries [16].
Literature studies aimed at characterizing new 3D printable stationary phases basically fall into three categories: (1) purely hydrodynamic studies in which the stationary phase is impermeable [11], [12], [13], [17], [18]; (2) studies in which the stationary phase is superficially activated/porous and thus only superficially adsorbent [9], [10], [19]; (3) studies in which the stationary phase is microporous and retentive [20], [21], [22], [23].
In this paper we investigated separation performances of eight different ordered monolithic stationary phases based on Triply Periodic Minimal Surfaces (TPMS) by addressing not only hydrodynamic dispersion (impermeable stationary phase) but also dispersion features in the wall-retentive case. Stationary phases based on TPMS have been already proposed as very promising geometries [17], [18]. Indeed, Dolamore et al. [18] investigated chromatographic performance of Schwarz Diamond, Schoën Gyroid and Schwarz Primitive stationary phases exclusively in the no-retentive case. We not only extended the analysis to five more TPMS geometries but also investigated how the presence of the stationary phase, assumed superficially retentive, modifies the separation performance of TPMS structures. The exact moment analysis method [24], [25], [26], [27] for the determination of the dispersion tensor in retentive porous media has been adopted to compute the dispersion coefficients, the plate height curves and the kinetic performance factors of all the geometries. Furthermore, a critical analysis of the effective possibility of 3D printing TPMS stationary phases has been performed, based on the comparison between the optimal unit cell dimension and the resolution that can be recently attained with 3D printing advanced techniques.
The article is organized as follows. Section 2 briefly reviews the transport equations that have been solved, via the Finite Element Method implemented by Comsol Multiphysics, to estimate the axial dispersion coefficient with the exact moment method. In Section 3 the eight different TPMS-based geometries are introduced. Their geometric and fluid dynamical characteristic parameters are presented in Section 4. Section 5 focuses on hydrodynamic dispersion data (no retention) while Section 6 analyzes dispersion properties in the case of surface retention. The analysis of the kinetic performance factors and kinetic plots, for all the TPMS-based geometries, is addressed in Section 7.
3. Geometries
Eight different geometries have been investigated: three strut-based TPMS, namely Schoen Gyroid (G), Schwarz Diamond (D), Schwarz Primitive (P) and five sheet-based TPMS, i.e. two Sheet Gyroids SGa and SGb, two Sheet Diamonds SDa and SDb, and one Sheet Primitive SPb [34], [35], [36], [37]. The structures of the stationary phase and the complementary mobile phase for all the geometries investigated are shown in Fig. 1 for Gyroids, Fig. 2 for Diamonds and Fig. 3 for Primitives.
 Journal of Chromatography A, Volume 1743, 2025, 465676: Fig. 1. Strut-based Gyroid (G) and sheet-based Gyroids (SGa and SGb): stationary phase (A,D,G), mobile phase (B,E,H) and normalized axial component of the fluid velocity field (C,F,I), being the seepage (interstitial) velocity along x.
Journal of Chromatography A, Volume 1743, 2025, 465676: Fig. 1. Strut-based Gyroid (G) and sheet-based Gyroids (SGa and SGb): stationary phase (A,D,G), mobile phase (B,E,H) and normalized axial component of the fluid velocity field (C,F,I), being the seepage (interstitial) velocity along x.
8. Conclusions
The chromatographic performance of eight different 3D printable non-porous stationary phases based on triply periodic minimal surfaces have been investigated in both no-retentive and superficially retentive cases. A detailed analysis of hydrodynamic dispersion data indicates that it is not possible to identify a single geometric or fluid-dynamic parameter that can explain, with no exceptions, the ordering of hydrodynamic performances. The analysis of plate height curves indicates that best performing geometries, namely SDa and SGb, in both the non-retentive and the retentive case, are associated with lower values of the effective diameter, and thus lower values of permeability, except for geometries affected by significant channeling phenomena. When compared in terms of kinetic performance factor, the best performing geometries are SPb, D and SGb, characterized by lower tortuosity and higher coefficient of uniformity of the axial velocity field. The analysis of the kinetic plot reveals that none of the geometries investigated can operate in optimal conditions (minimum of the kinetic plot) because this would require to diminish the dimension of the unit cell below the limits dictated by the minimum feature size of the currently available 3D printing techniques. However, this finding should not suggest that TPMS geometries are not promising candidates for practical efficient chromatography. In fact, several studies [20], [21], [22] have already shown the possibility of 3D printing microporous stationary phases. The contribution of the internal porosity of the stationary phase to the separation properties is of fundamental importance and can drastically change the chromatographic performance of novel stationary phases based on triply periodic minimal surfaces [46].